A Family Has Five Kids. What Is the Probability That They Consist of 2 Boys and 3 Girls

Probability for Rolling Two Die

Probability for rolling two dice with the six sided dots such as 1, 2, 3, 4, 5 and 6 dots in each dice.

When two dice are thrown simultaneously, thus number of outcome can be 6² = 36 because each die has 1 to 6 number on its faces. Then the possible outcomes are shown in the beneath tabular array.

Probability – Sample infinite for 2 dice (outcomes):

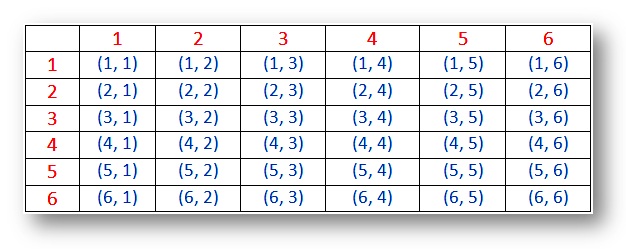
Note:

(i) The outcomes (1, ane), (2, two), (three, 3), (4, 4), (v, v) and (6, vi) are called doublets.

(ii) The pair (one, 2) and (two, 1) are dissimilar outcomes.

Worked-out bug involving probability for rolling two dice:

1. Ii dice are rolled. Let A, B, C be the events of getting a sum of 2, a sum of 3 and a sum of four respectively. Then, testify that

(i) A is a simple event

(ii) B and C are chemical compound events

(3) A and B are mutually exclusive

Solution:

Clearly, we have
A = {(1, 1)}, B = {(1, 2), (2, 1)} and C = {(ane, 3), (3, 1), (two, 2)}.

(i) Since A consists of a single sample point, information technology is a simple event.

(ii) Since both B and C contain more than than one sample point, each ane of them is a chemical compound event.

(three) Since A ∩ B = ∅, A and B are mutually exclusive.

2. Two dice are rolled. A is the event that the sum of the numbers shown on the two dice is 5, and B is the outcome that at to the lowest degree i of the die shows up a 3.
Are the two events (i) mutually sectional, (ii) exhaustive? Give arguments in support of your answer.

Solution:

When two dice are rolled, we have northward(South) = (vi × half dozen) = 36.

Now, A = {(1, 4), (2, 3), (4, 1), (3, 2)}, and

B = {(3, 1), (iii, two), (three, iii), (3, 4), (3, 5), (three, 6), (1,3), (ii, 3), (4, 3), (v, iii), (6, 3)}

(i) A ∩ B = {(2, three), (3, two)} ≠ ∅.

Hence, A and B are not mutually sectional.

(two) Also, A ∪ B ≠ South.

Therefore, A and B are not exhaustive events.

More than examples related to the questions on the probabilities for throwing ii die.

iii. Two dice are thrown simultaneously. Find the probability of:

(i) getting six as a production

(ii) getting sum ≤ 3

(iii) getting sum ≤ x

(4) getting a doublet

(5) getting a sum of viii

(half-dozen) getting sum divisible past v

(7) getting sum of atleast 11

(viii) getting a multiple of 3 equally the sum

(9) getting a full of atleast ten

(10) getting an even number as the sum

(eleven) getting a prime number number as the sum

(xii) getting a doublet of even numbers

(thirteen) getting a multiple of 2 on one die and a multiple of 3 on the other die

Solution:

Ii unlike dice are thrown simultaneously being number one, 2, iii, 4, 5 and half dozen on their faces. We know that in a unmarried thrown of two different die, the total number of possible outcomes is (half dozen × 6) = 36.

(i) getting 6 as a product:

Let E₁ = result of getting six as a product. The number whose product is six will be E_one = [(one, half-dozen), (2, 3), (three, 2), (6, 1)] = four

Therefore, probability of getting 'six every bit a product'

               Number of favorable outcomes
P(E₁) = Total number of possible outcome

= 4/36
= one/9

(two) getting sum ≤ iii:

Permit E₂ = event of getting sum ≤ 3. The number whose sum ≤ 3 will be E₂ = [(ane, i), (1, 2), (2, ane)] = 3

Therefore, probability of getting 'sum ≤ 3'

               Number of favorable outcomes
P(Due east_two) = Total number of possible outcome

= 3/36
= 1/12

(iii) getting sum ≤ ten:

Permit Due east_iii = outcome of getting sum ≤ ten. The number whose sum ≤ x will be East_iii =

[(1, 1), (1, 2), (i, iii), (1, iv), (1, 5), (1, 6),

(2, i), (2, ii), (2, 3), (2, iv), (2, 5), (ii, 6),

(iii, ane), (three, two), (three, 3), (3, iv), (iii, 5), (three, 6),

(4, 1), (4, 2), (4, 3), (4, iv), (4, 5), (4, six)

(5, 1), (5, 2), (five, 3), (v, iv), (5, 5),

(vi, ane), (6, 2), (6, 3), (half dozen, four)] = 33

Therefore, probability of getting 'sum ≤ ten'

               Number of favorable outcomes
P(E₃) = Full number of possible outcome

= 33/36
= 11/12

(iv) getting a doublet: Permit E₄ = issue of getting a doublet. The number which doublet will be E_iv = [(1, 1), (2, 2), (3, 3), (four, four), (five, 5), (6, 6)] = vi

Therefore, probability of getting 'a doublet'

               Number of favorable outcomes
P(E₄) = Total number of possible outcome

= 6/36
= i/vi

(v) getting a sum of 8:

Let Due east_five = result of getting a sum of 8. The number which is a sum of 8 will be E₅ = [(2, 6), (3, 5), (four, 4), (5, 3), (vi, ii)] = 5

Therefore, probability of getting 'a sum of 8'

               Number of favorable outcomes
P(E_v) = Total number of possible result

= 5/36

(vi) getting sum divisible past 5:

Allow E_half-dozen = event of getting sum divisible past 5. The number whose sum divisible by 5 will be E₆ = [(1, four), (2, 3), (3, two), (4, 1), (4, six), (5, 5), (six, four)] = seven

Therefore, probability of getting 'sum divisible past 5'

               Number of favorable outcomes
P(E_six) = Total number of possible outcome

= 7/36

(vii) getting sum of atleast eleven:

Let E₇ = result of getting sum of atleast 11. The events of the sum of atleast 11 will be E₇ = [(five, 6), (half dozen, v), (6, half dozen)] = three

Therefore, probability of getting 'sum of atleast 11'

               Number of favorable outcomes
P(E_vii) = Total number of possible issue

= three/36
= 1/12

(8) getting a multiple of 3 as the sum:

Let E_eight = outcome of getting a multiple of 3 as the sum. The events of a multiple of 3 as the sum will be E₈ = [(ane, 2), (1, 5), (two, ane), (2, iv), (three, 3), (3, vi), (4, 2), (4, 5), (5, 1), (v, 4), (vi, iii) (six, six)] = 12

Therefore, probability of getting 'a multiple of 3 equally the sum'

               Number of favorable outcomes
P(E_eight) = Total number of possible event

= 12/36
= 1/3

(ix) getting a total of atleast 10:

Permit E_ix = effect of getting a total of atleast x. The events of a total of atleast ten volition exist Due east₉ = [(iv, 6), (5, five), (5, 6), (6, 4), (6, 5), (6, 6)] = 6

Therefore, probability of getting 'a total of atleast 10'

               Number of favorable outcomes
P(East₉) = Total number of possible outcome

= vi/36
= 1/6

(x) getting an even number every bit the sum:

Permit Eastward₁₀ = event of getting an fifty-fifty number as the sum. The events of an even number every bit the sum will be E₁₀ = [(one, i), (i, iii), (one, five), (2, ii), (2, iv), (2, 6), (iii, iii), (three, 1), (three, 5), (4, 4), (4, 2), (4, six), (v, ane), (5, 3), (5, 5), (half dozen, 2), (6, 4), (6, half-dozen)] = 18

Therefore, probability of getting 'an fifty-fifty number as the sum

               Number of favorable outcomes
P(E₁₀) = Full number of possible outcome

= eighteen/36
= 1/two

(xi) getting a prime number as the sum:

Let E_xi = issue of getting a prime number number as the sum. The events of a prime number as the sum will be E_xi = [(ane, 1), (ane, two), (1, 4), (one, six), (2, 1), (2, iii), (2, 5), (three, 2), (3, 4), (iv, one), (4, 3), (5, ii), (5, 6), (six, ane), (6, 5)] = fifteen

Therefore, probability of getting 'a prime as the sum'

               Number of favorable outcomes
P(E_xi) = Total number of possible outcome

= 15/36
= 5/12

(xii) getting a doublet of even numbers:

Let E₁₂ = effect of getting a doublet of fifty-fifty numbers. The events of a doublet of even numbers will be Eastward₁₂ = [(2, ii), (four, 4), (6, 6)] = 3

Therefore, probability of getting 'a doublet of even numbers'

               Number of favorable outcomes
P(E₁₂) = Total number of possible outcome

= 3/36
= ane/12

(13) getting a multiple of 2 on one die and a multiple of three on the other dice:

Let E₁₃ = consequence of getting a multiple of 2 on one dice and a multiple of iii on the other die. The events of a multiple of 2 on one die and a multiple of 3 on the other die will be Due east_thirteen = [(two, three), (2, vi), (3, 2), (iii, 4), (3, half-dozen), (4, 3), (4, six), (vi, ii), (6, iii), (6, 4), (6, vi)] = 11

Therefore, probability of getting 'a multiple of two on one die and a multiple of 3 on the other dice'

               Number of favorable outcomes
P(East_thirteen) = Full number of possible issue

= xi/36

4. Two dice are thrown. Find (i) the odds in favour of getting the sum five, and (2) the odds against getting the sum vi.

Solution:

We know that in a single thrown of two die, the total number of possible outcomes is (6 × 6) = 36.

Allow S be the sample space. Then, n(Due south) = 36.

(i) the odds in favour of getting the sum 5:

Let East_one be the result of getting the sum v. Then,
E₁ = {(1, 4), (2, three), (3, 2), (4, 1)}
⇒ P(Eastward_i) = four
Therefore, P(E₁) = n(Eastward₁)/north(S) = 4/36 = one/9
⇒ odds in favour of E₁ = P(E₁)/[i – P(Due east₁)] = (ane/9)/(1 – 1/9) = i/8.

(ii) the odds against getting the sum vi:

Let Due east₂ exist the event of getting the sum 6. And then,
East₂ = {(i, 5), (2, 4), (three, 3), (4, 2), (5, one)}
⇒ P(E_two) = v
Therefore, P(E_two) = due north(E₂)/n(S) = five/36
⇒ odds against Due east₂ = [1 – P(E_ii)]/P(E_two) = (1 – 5/36)/(five/36) = 31/5.

5. Two dice, one blue and i orange, are rolled simultaneously. Find the probability of getting

(i) equal numbers on both

(2) two numbers appearing on them whose sum is ix.

Solution:

The possible outcomes are

(1, 1), (1, ii), (i, iii), (1, four), (ane, 5), (1, 6),

(2, ane), (ii, ii), (2, 3), (2, iv), (2, 5), (2, half-dozen),

(3, 1), (3, 2), (3, 3), (3, four), (iii, 5), (three, half-dozen),

(four, one), (4, 2), (4, 3), (4, four), (iv, 5), (iv, half-dozen)

(five, i), (5, ii), (five, 3), (five, 4), (five, 5), (5, 6)

(6, 1), (half dozen, two), (half dozen, iii), (6, iv), (6, 5), (6, 6)

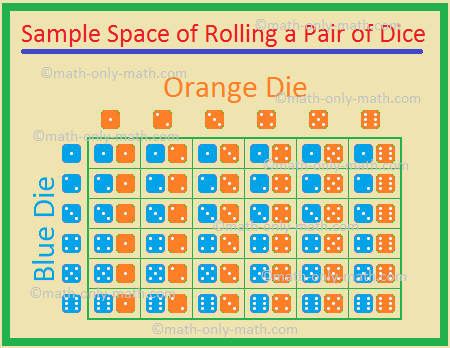
Therefore, full number of possible outcomes = 36.

(i) Number of favourable outcomes for the upshot Eastward

                   = number of outcomes having equal numbers on both dice

                   = half-dozen    [namely, (1, 1), (2, two), (3, three), (iv, four), (v, 5), (6, vi)].

So, by definition, P(E) = \(\frac{6}{36}\)

                                 = \(\frac{i}{half dozen}\)

(two) Number of favourable outcomes for the result F

           = Number of outcomes in which two numbers actualization on them have the sum 9

            = iv     [namely, (3, 6), (iv, 5), (5, 4), (iii, 6)].

Thus, by definition, P(F) = \(\frac{4}{36}\)

                                    = \(\frac{1}{ix}\).

These examples will assist us to solve different types of problems based on probability for rolling two dice.

Probability

Probability

Random Experiments

Experimental Probability

Events in Probability

Empirical Probability

Money Toss Probability

Probability of Tossing Two Coins

Probability of Tossing Three Coins

Free Events

Mutually Exclusive Events

Mutually Non-Exclusive Events

Conditional Probability

Theoretical Probability

Odds and Probability

Playing Cards Probability

Probability and Playing Cards

Probability for Rolling Two Die

Solved Probability Problems

Probability for Rolling Three Dice

9th Course Math

From Probability for Rolling Two Dice to HOME Folio

Didn't find what you were looking for? Or desire to know more data about Math Only Math. Employ this Google Search to find what yous need.

bennettdiell1982.blogspot.com

Source: https://www.math-only-math.com/probability-for-rolling-two-dice.html